강화학습 알고리즘 과정 참조
머신러닝교과서with파이썬,사이킷런,텐서플로_개정3판pg786
동적 계획법
전이 동역학(환경 동역학)이 알려져 있다고 가정할 경우 동적 계획법을 먼저 다룬다.(대부분의 강화 학습 문제는 해당하지 않음)
몬테카를로
전이 동역학을 모를 경우 환경과 상호 작용을 함
시간 차
MC 방법을 향상시킨 것으로 매 단계마다 가치 함수를 업데이트 한다.
온-폴리시: SARSA
오프-폴리시: Q-러닝
- 동적 계획법
환경 동역학에 대해 완벽하게 알고 있다.(모든 전이 확률(s’, r | s, a)를 알 수 있다.)
에이전트의 상태는 마르코프의 성질을 가진다.(다음 행동과 보상은 오직 현재 상태와 현재 타입 스텝에서
선택한 행동에 의해서만 결정)
동적 계획법은 강화 학습 문제를 풀기 위한 실용적인 방법이 아니다.
동적 계획법을 사용할 때는 환경 동역학을 완벽히 알고 있다고 가정한다.(실제로는 적절하지 않고 비현실적임)
두 가지 목표
1. 진짜 상태-가치 함수 구하기: 예측작업이라고 하며 정책 평가로 구할 수 있다.
2. 최적의 가치 함수 찾기: 일반화된 정책 반복을 통해 얻을 수 있다.
정책 평가: 동적 계획법으로 가치 함수 예측
벨먼 방정식을 기반으로 임의의 정책을 위한 가치 함수를 동적 계획법으로 계산할 수 있다.

점화식 형태로 가치 함수를 업데이트
v<i>(s)는 반복을 거쳐서 상태-가치 함수 v_pi(s)로 수렴
환경 동역학을 정확하고 알고 있기 때문에 환경과 상호 작용을 필요로 하지는 않는다.
가치 함수로 정책 향상(정책 향상 policy improvement 알고리즘)
기존 정책에 대한 가치 함수 v_pi(s)를 사용해서 기존의 정책 pi를 향상시킬려고 할 경우
현재 정책 pi를 사용할 때보다 더 높거나 최소한 같은 가치를 만드는 새로운 정책 pi’를 찾는다.
모든 상태에서 항상 더 높거나 같은 가치를 가지는 pi’를 찾기 위해서
가치 함수 v_pi(s)로 계산한 상태함수를 기반으로 상태 s와 행동 a에 대한 행동-가치 함수 q_pi(s, a)를 계산해야 한다.
각 상태 s에서 행동 a를 선택했을 때, 다음 상태 s’의 가치와 비교한다.
q_pi(s)로 모든 상태-가치 쌍을 계산하여 가장 높은 상태 가치를 얻은 후,
현재 정책이 선택한 행동과 비교한다.
현재 정책이 선택한 행동(arg max pi(a|s))과 행동-가치 함수로 계산한 행동(arg max q_pi(s, a))이 다르면,
가장 높은 행동 가치 q_pi(s, a)를 만드는 행동에 맞도록 행동의 확률을 다시 할당-정책 향상(policy improvement 알고리즘)
정책 반복
정책 향상 알고리즘을 이용하면, 현재 정책이 이미 최적이 아닐 경우 정책 향상은 더 나은 정책을 만들 수 있다.
정책 향상 알고리즘을 따라 정책 평가를 반복적으로 수행하면, 최적의 정책을 찾을 수 있다는 것이 보장된다.
Generalized Policy Iteration, GPI: 많은 강화 학습 기법에 널리 사용되고 있음-MC, TD 등
가치 반복
정책 평가와 정책 향상을 반복적으로 사용함으로서 최적의 정책에 도달할 수 있다.
정책 평가와 정책 향상을 하나의 단계로 합치면 훨씬 효율적이다.

가중치 합(r+gamma*v<i>(s’))을 최대화하는 행동에 기반하여 반복 i+1에서 가치 함수 v<i+1>을 업데이트
v<i+1>(s)는 가능한 모든 행동 중에서 최선의 행동을 선택하면서 최대화된다.
정책 평가에서는 업데이트된 모든 가치가 모든 행동에 대한 가중치 합을 사용
- 몬테카를로(Monte Carlo, MC)
환경 동역학에 대한 정보가 전혀 없을 경우(환경의 상태-전이 확률을 모름)
에이전트는 환경과 상호작용을 통해서 학습해야 한다. MC는 모의 경험(simulated experience)를 기반으로 한다.
MC 기반의 강화 학습에서는 확률적인 정책 pi를 따르는 에이전트 클래스를 정의한다.
(정책을 기반으로 에이전트는 매 단계의 행동을 선택-이를 통해 모의 에피스드(simulated episode)를 만든다.)
MC 기반 방법은 에이전트가 환경 동역학 지식(p(s’, r | s, a)를 사용할 수 없다.
대신 에이전트가 환경과 상호 작용할 모의 에피소드를 생성하여 문제를 해결한다.
-> 모의 에피소드에 방문한 각 상태의 평균 대가를 계산
MC를 사용한 상태-가치 함수 추정
환경 동역학을 알고 있으면, ‘동적 계산법’ 처럼 최대가치를 주는 행동을 찾아 상태-가치 함수로부터 행동-가치 함수를
추정할 수 있다.
환경 동역학을 모를 경우 행동-가치 함수를 사용하여 상태-행동 쌍에 대한 추정 대가를 계산한다.
추정한 대가를 얻기 위해 각 상태-행동 쌍 (s, a)를 방문한다.(상태 s를 선택해서 행동 a를 선택)
일부 행동은 전혀 선택되지 않을 경우 충분한 탐험이 이루어 지지 않는다.
에피소드를 시작할 때 모든 상태-행동 쌍이 0이 아닌 확률을 가진다고 가정하는 탐험적 시작(exploratory start)을
통해 해결할 수 있다.
MC 제어를 사용하여 최적의 정책 찾기
MC 제어(control)는 정책을 향상시키기 위한 최적화 과정을 의미한다.
최적의 정책에 도달할 때까지 정책 평가와 정책 향상을 교대로 반복한다.
정책 향상: 행동-가치 함수로부터 그리디 정책 계산
행동-가치 함수 q(s, a)가 주어지면 아래와 같은 그리디 정책을 만든다.

탐험 부족 문제를 피하기 위해서 방문하지 않은 상태-행동 쌍을 고려하기 위해 최적이 아닌 행동에
약간의 선택 기회(epsilon)를 줄 수 있다. (epsilon-그리디 정책)
상태 s에서 최적이 아닌 모든 행동은 0이 아닌 적어도 epsilon/abs(A(s))의 선택 확률을 가진다.
- 시간 차 학습(Temporal difference)
TD학습은 MC 기반 강화 학습의 향상 또는 확장 버전으로 볼 수 있다.
MC 방법과 유사하게 TD 학습도 경험을 통해 이루어진다.(환경 동이학과 전이 확률에 대한 지식 필요 없음)
TD는 MC와 달리 총 대가를 계산하기 위해 에피소드가 끝날 때까지 기다릴 필요가 없다.
부트 스트래핑(bootstrapping)
TD 학습에서는 에프소드 끝에 도달하기 전에 몇 가지 학습된 성지릉 사용하여 추정된 가치를 업데이트 할 수 있다.
TD 예측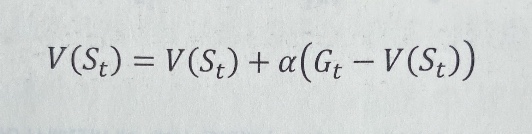
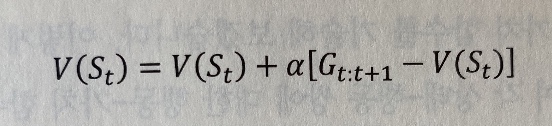
MC에서 각 에피소드 끝에서 타임 스텝 t에 대한 대가 G_t를 추정할 수 있다.
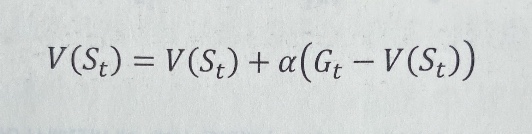
방문에 대한 추정 값을 위와 같이 업데이트한다.(alpha는 학습률 하이퍼파라미터)
MC에서는 G_t는 에피소드가 끝날 때까지 알 수가 없다.(t=T)
TD 학습에서는 실제 대가 G_t:T를 새로운 타깃 대가 G_t:t+1로 바꾸어 가치 함ㅅ루 V(S_t)를 위한 업데이트를 단순화 한다.
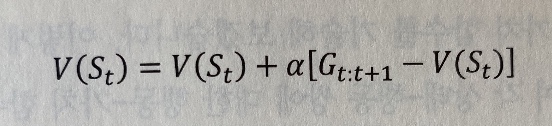
G_t:t+1=
MC & TD
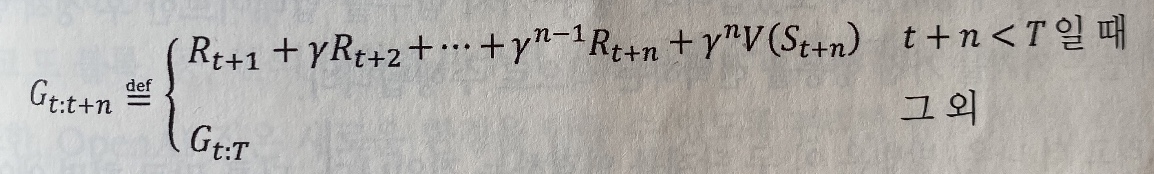
MC에서는 G_t:T를 에피소드가 끝날 때까지 알 수 가 없다.
따라서 에피소드가 끝날 때까지 필요한 만큼 많은 단계를 실행해야 한다.
TD에서는 타깃 대가를 얻기 위해 한 단계만 앞서 실행하면 된다. (TD(0))
미래 n 스텝의 가중치 하블 사용한다.(n->infinite 이면 n-스텝 TD 알고리즘은 MC 알고리즘과 동일)
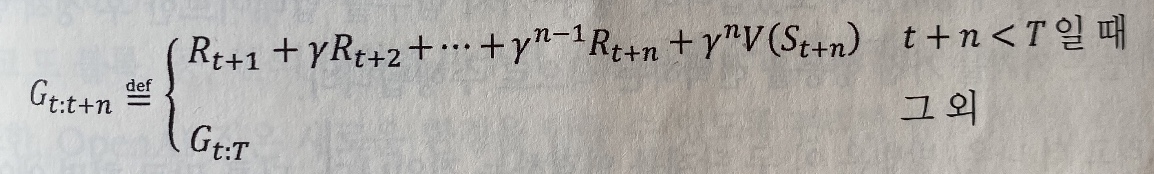
TD 제어(온-폴리시 TD, 오프-폴리시 TD)
- 온-폴리시 TD 제어(SARSA)
온-폴리시 TD 제어 알고리즘은 n-스텝 TD로 쉽게 일반화 할 수 있다.

룩업 테이블, 2D 배열 Q(S_t, A_t)를 사용해서 각 상태-행동 쌍에 대한 행동-가치 함수를 표현(SARSA 알고리즘)
랜덤한 저책으로 시작해서 반복적으로 현재 정책의 행동-가치 함수를 추정
현재의 행동-가치 함수를 기반으로 episilon-그리디 정책을 사용해서 정책을 최적화
- 오프-폴리시 TD 제어(Q-Learning)

온 폴리시는 모의 에피소드에서 사용한 정책을 기반으로 행동-가치 함수를 추정하였다.
행동-가치 함수를 업데이트한 후 정책 향상은 별도의 단계에서 높은 가치를 가진 행동을 선택한다.
오프-폴리시 제어는 위 두 단계를 연결한다.
현재의 전이 원소(S_t, A_t, R_t+1, S_t+1, A_t+1)로 에피소드를 생성하면서 정책 pi를 따른다고 할 때,
에이전트가 선택한 A_t+1의 행동 가치를 사용하여 행동-가치 함수를 업데이트하는 대신
현재 정책을 따르는 에이전트가 실제로 선택한 것이 아니더라도 최선의 행동을 찾을 수 있다.
여러 행동에 대한 최대 Q-가치를 고려하도록 업데이트 공식을 수정
